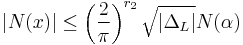Ideal norm
In commutative algebra, the norm of an ideal is a generalization of a norm of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal of a complicated number ring in terms of an ideal in a less complicated ring. When the less complicated number ring is taken to be the ring of integers, Z, then the norm of a nonzero ideal I of a number ring R is simply the size of the finite quotient ring R/I.
Contents |
Relative norm
Let A be a Dedekind domain with the field of fractions K and B be the integral closure of A in a finite separable extension L of K. (In particular, B is Dedekind then.) Let 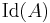 and
and 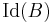 be the ideal groups of A and B, respectively (i.e., the sets of fractional ideals.) Following (Serre 1979), the norm map
be the ideal groups of A and B, respectively (i.e., the sets of fractional ideals.) Following (Serre 1979), the norm map
is a homomorphism given by
If 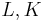 are local fields,
are local fields, 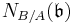 is defined to be a fractional ideal generated by the set
is defined to be a fractional ideal generated by the set 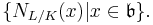 This definition is equivalent to the above and is given in (Iwasawa 1986).
This definition is equivalent to the above and is given in (Iwasawa 1986).
For 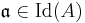 , one has
, one has 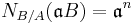 where
where ![n = [L�: K]](/2012-wikipedia_en_all_nopic_01_2012/I/ae2ac22ceecdd70128076c7e2d5e6f6f.png) . The definition is also compatible with norm of an element:
. The definition is also compatible with norm of an element: 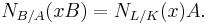 [1]
[1]
Let 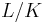 be a finite Galois extension of number fields with rings of integers
be a finite Galois extension of number fields with rings of integers 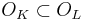 . Then the preceding applies with
. Then the preceding applies with 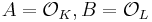 and one has
and one has
which is an ideal of 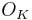 . The norm of a principal ideal generated by α is the ideal generated by the field norm of α.
. The norm of a principal ideal generated by α is the ideal generated by the field norm of α.
The norm map is defined from the set of ideals of 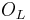 to the set of ideals of
to the set of ideals of 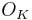 . It is reasonable to use integers as the range for
. It is reasonable to use integers as the range for  since Z has trivial ideal class group. This idea does not work in general since the class group may not be trivial.
since Z has trivial ideal class group. This idea does not work in general since the class group may not be trivial.
Absolute norm
Let  be a number field with ring of integers
be a number field with ring of integers 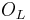 , and
, and  a nonzero ideal of
a nonzero ideal of 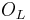 . Then the norm of
. Then the norm of  is defined to be
is defined to be
By convention, the norm of the zero ideal is taken to be zero.
If  is a principal ideal with
is a principal ideal with 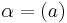 , then
, then 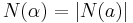 .
.
The norm is also completely multiplicative in that if  and
and  are ideals of
are ideals of 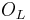 , then
, then 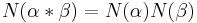 .
.
The norm of an ideal  can be used to bound the norm of some nonzero element
can be used to bound the norm of some nonzero element 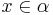 by the inequality
by the inequality
where 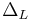 is the discriminant of
is the discriminant of  and
and 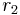 is the number of pairs of complex embeddings of
is the number of pairs of complex embeddings of  into
into 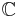 .
.
See also
References
- ^ Serre, 1. 5, Proposition 14.
- Iwasawa, Kenkichi (1986), Local class field theory, Oxford Science Publications, New York: The Clarendon Press Oxford University Press, pp. viii+155, ISBN 0-19-504030-9, MR(88b:11080) 863740 (88b:11080)
- Marcus, Daniel A. (1977), Number fields, New York: Springer-Verlag, pp. viii+279, ISBN 0-387-90279-1, MR(56 #15601) 0457396 (56 #15601)
- Serre, Jean-Pierre (1979), Local fields},, Graduate Texts in Mathematics, 67, New York: Springer-Verlag, pp. viii+241, ISBN 0-387-90424-7, MR(82e:12016) 554237 (82e:12016)
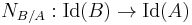
![N_{B/A}(\mathfrak q) = \mathfrak{p}^{[B/\mathfrak q�: A/\mathfrak p]}, \mathfrak q \in \operatorname{Spec} B, \mathfrak q | \mathfrak p.](/2012-wikipedia_en_all_nopic_01_2012/I/151116f2b6651ae2e09e7b11b082acc8.png)
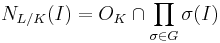
![N(\alpha) =\left [ O_L: \alpha\right ]=|O_L/\alpha|.\,](/2012-wikipedia_en_all_nopic_01_2012/I/5cf416bc41df9c09d19a824a3e17038b.png)